Xem lại chương 3
Bài 7 trang 107 SGK Đại số 11
Xem xét các tính chất tăng, giảm và giới hạn của dãy số (uN), biết:
Câu trả lời
Hướng dẫn
*) Xem xét hiệu ứng un + 1-uN
Nếu sự khác lạ là số dương, thì chuỗi là một chuỗi tăng dần.
Nếu sự khác lạ là âm, thì chuỗi là một chuỗi giảm dần.
Nếu hiệu trên bằng 0, thì dãy đó là dãy ko đổi.
*) Dãy số (uN) được cho là giới hạn trên nếu tồn tại một số M sao cho uN M n
Chuỗi số (uN) được cho là giới hạn dưới nếu tồn tại một số m sao cho un mn N ∗
Dãy (un) được cho là có giới hạn nếu nó bị ràng buộc cả trên và dưới, tức là tồn tại các số M, m sao cho m un ≤ M ∀n ∈ N ∗
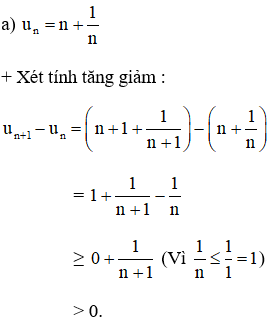
un + 1 > uN cho tất cả n phụ nữ
(uN) là một chuỗi tăng dần.
+ Xem xét chặn:
(uN) là một chuỗi ngày càng tăng
uTrước hết = 2 2 3 nn N *
uN 2 n N *
(uN) được ràng buộc bên dưới.
(uN) ko bị chặn trên.
uN ko bị chặn.
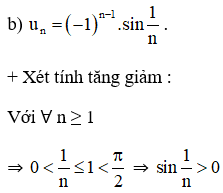
Suy luận: Với nn chẵn – 1 lẻ (-1)n – 1 = -1 uN
Đối với n lẻ n – 1 chẵn (-1)n – 1 = 1 uN > 0.
uTrước hết > u2 3> u4 5> u6 …
(uN) ko tăng cũng ko giảm.
+ Xem xét chặn:
Với ∀ n ∈ N:
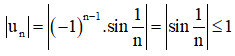
-1 uN ≤ 1.
Vì vậy (uN) bị chặn.
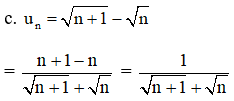
+ Cân nhắc sự tăng giảm.
Với mọi n ∈ N, ta có:
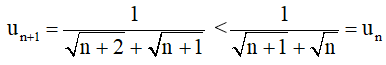
un + 1 n với mọi n ∈ N.
(uN) là một chuỗi giảm dần.
+ Xem xét việc ngăn chặn.
uN > 0 với mọi n.
(uN) được ràng buộc bên dưới.
uN uTrước hết = 2 – 1 cho tất cả n
(uN) bị chặn vào.
(uN) bị chặn.
Nhìn thấy tất cả Giải Toán 11: Ôn tập chương 3
Đăng bởi: Trường Trường THPT Trần Hưng Đạo
Phân mục: Toán lớp 11, Toán 11
[toggle title=”xem thêm thông tin chi tiết về Bài 7 trang 107 SGK Đại số 11 ” state=”close”]
Bài 7 trang 107 SGK Đại số 11
Hình Ảnh về: Bài 7 trang 107 SGK Đại số 11
Video về: Bài 7 trang 107 SGK Đại số 11
Wiki về Bài 7 trang 107 SGK Đại số 11
Bài 7 trang 107 SGK Đại số 11 -
Xem lại chương 3
Bài 7 trang 107 SGK Đại số 11
Xem xét các tính chất tăng, giảm và giới hạn của dãy số (uN), biết:
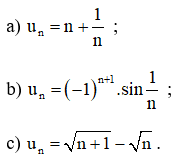
Câu trả lời
Hướng dẫn
*) Xem xét hiệu ứng un + 1-uN
Nếu sự khác lạ là số dương, thì chuỗi là một chuỗi tăng dần.
Nếu sự khác lạ là âm, thì chuỗi là một chuỗi giảm dần.
Nếu hiệu trên bằng 0, thì dãy đó là dãy ko đổi.
*) Dãy số (uN) được cho là giới hạn trên nếu tồn tại một số M sao cho uN M n
Chuỗi số (uN) được cho là giới hạn dưới nếu tồn tại một số m sao cho un mn N ∗
Dãy (un) được cho là có giới hạn nếu nó bị ràng buộc cả trên và dưới, tức là tồn tại các số M, m sao cho m un ≤ M ∀n ∈ N ∗
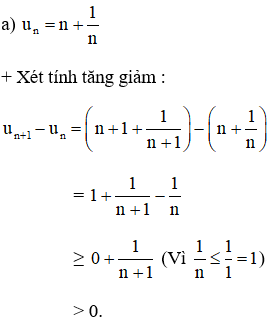
un + 1 > uN cho tất cả n phụ nữ
(uN) là một chuỗi tăng dần.
+ Xem xét chặn:
(uN) là một chuỗi ngày càng tăng
uTrước hết = 2 2 3 nn N *
uN 2 n N *
(uN) được ràng buộc bên dưới.
(uN) ko bị chặn trên.
uN ko bị chặn.
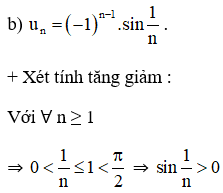
Suy luận: Với nn chẵn - 1 lẻ (-1)n - 1 = -1 uN
Đối với n lẻ n - 1 chẵn (-1)n - 1 = 1 uN > 0.
uTrước hết > u2 3> u4 5> u6 …
(uN) ko tăng cũng ko giảm.
+ Xem xét chặn:
Với ∀ n ∈ N:
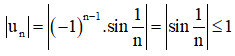
-1 uN ≤ 1.
Vì vậy (uN) bị chặn.
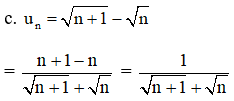
+ Cân nhắc sự tăng giảm.
Với mọi n ∈ N, ta có:
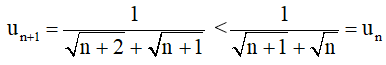
un + 1 n với mọi n ∈ N.
(uN) là một chuỗi giảm dần.
+ Xem xét việc ngăn chặn.
uN > 0 với mọi n.
(uN) được ràng buộc bên dưới.
uN uTrước hết = 2 - 1 cho tất cả n
(uN) bị chặn vào.
(uN) bị chặn.
Nhìn thấy tất cả Giải Toán 11: Ôn tập chương 3
Đăng bởi: Trường Trường THPT Trần Hưng Đạo
Phân mục: Toán lớp 11, Toán 11
[rule_{ruleNumber}]
[box type=”note” align=”” class=”” color: #194fbd;”>Bài 7 trang 107 SGK Đại số 11
Xem xét các thuộc tính tăng, giảm và giới hạn của dãy số (uN), biết:
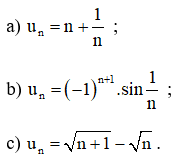
Câu trả lời
Hướng dẫn
*) Xem xét hiệu ứng un + 1-uN
Nếu sự khác biệt là số dương, thì chuỗi là một chuỗi tăng dần.
Nếu sự khác biệt là âm, thì chuỗi là một chuỗi giảm dần.
Nếu hiệu trên bằng 0, thì dãy đó là dãy không đổi.
*) Dãy số (uN) được cho là giới hạn trên nếu tồn tại một số M sao cho uN M n
Chuỗi số (uN) được cho là giới hạn dưới nếu tồn tại một số m sao cho un mn N ∗
Dãy (un) được cho là có giới hạn nếu nó bị ràng buộc cả trên và dưới, tức là tồn tại các số M, m sao cho m un ≤ M ∀n ∈ N ∗
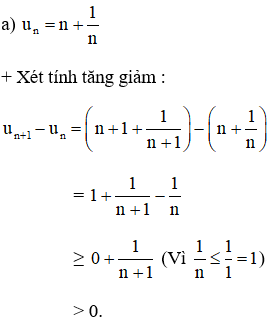
un + 1 > uN cho tất cả n phụ nữ
(uN) là một chuỗi tăng dần.
+ Xem xét chặn:
(uN) là một chuỗi ngày càng tăng
uĐầu tiên = 2 2 3 nn N *
uN 2 n N *
(uN) được ràng buộc bên dưới.
(uN) không bị chặn trên.
uN không bị chặn.
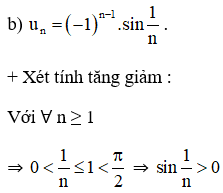
Suy luận: Với nn chẵn – 1 lẻ (-1)n – 1 = -1 uN
Đối với n lẻ n – 1 chẵn (-1)n – 1 = 1 uN > 0.
uĐầu tiên > u2 3> u4 5> u6 …
(uN) không tăng cũng không giảm.
+ Xem xét chặn:
Với ∀ n ∈ N:
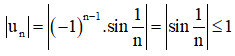
-1 uN ≤ 1.
Vì vậy (uN) bị chặn.
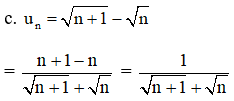
+ Cân nhắc sự tăng giảm.
Với mọi n ∈ N, ta có:
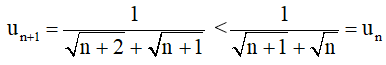
un + 1 n với mọi n ∈ N.
(uN) là một chuỗi giảm dần.
+ Xem xét việc ngăn chặn.
uN > 0 với mọi n.
(uN) được ràng buộc bên dưới.
uN uĐầu tiên = 2 – 1 cho tất cả n
(uN) bị chặn vào.
(uN) bị chặn.
Nhìn thấy tất cả Giải Toán 11: Ôn tập chương 3
Đăng bởi: Trường Trường THPT Trần Hưng Đạo
Chuyên mục: Toán lớp 11, Toán 11
[/box]
#Bài #trang #SGK #Đại #số
[rule_3_plain]
#Bài #trang #SGK #Đại #số
Ôn tập chương 3
Bài 7 trang 107 SGK Đại số 11
Xét tính tăng, giảm và bị chặn của các dãy số (un), biết:
Lời giải
Hướng dẫn
*) Xét hiệu un+1−un
Nếu hiệu trên dương thì dãy số là dãy số tăng.
(adsbygoogle = window.adsbygoogle || []).push({});
Nếu hiệu trên âm thì dãy số là dãy số giảm.
Nếu hiệu trên bằng 0 thì dãy số là dãy ko đổi.
*) Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho un ≤ M ∀n ∈ N∗
Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho un ≥ m ∀n ∈ N∗
Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số M, m sao cho m ≤ un ≤ M ∀n ∈ N∗
(adsbygoogle = window.adsbygoogle || []).push({});
⇒ un + 1 > un với mọi n ∈ N
⇒ (un) là dãy tăng.
+ Xét tính bị chặn:
(un) là dãy tăng
⇒ u1 = 2 2 3 n ∀n ∈ N*
⇒ un ≥ 2 ∀n ∈ N*
⇒ (un) bị chặn dưới.
(un) ko bị chặn trên.
⇒ un ko bị chặn.
Suy ra: Với n chẵn ⇒ n – 1 lẻ ⇒ (-1)n – 1 = -1 ⇒ un
Với n lẻ ⇒ n – 1 chẵn ⇒ (-1)n – 1 = 1 ⇒ un > 0.
⇒ u1 > u2 3 > u4 5 > u6 …
⇒ (un) ko tăng ko giảm.
+ Xét tính bị chặn :
Với ∀ n ∈ N:
⇒ -1 ≤ un ≤ 1.
Vậy (un) bị chặn.
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
⇒ un + 1 n với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 – 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Xem toàn thể Giải Toán 11: Ôn tập chương 3
Đăng bởi: Trường THPT Trần Hưng Đạo
Phân mục: Lớp 11, Toán 11
#Bài #trang #SGK #Đại #số
[rule_2_plain]
#Bài #trang #SGK #Đại #số
[rule_2_plain]
#Bài #trang #SGK #Đại #số
[rule_3_plain]
#Bài #trang #SGK #Đại #số
Ôn tập chương 3
Bài 7 trang 107 SGK Đại số 11
Xét tính tăng, giảm và bị chặn của các dãy số (un), biết:
Lời giải
Hướng dẫn
*) Xét hiệu un+1−un
Nếu hiệu trên dương thì dãy số là dãy số tăng.
(adsbygoogle = window.adsbygoogle || []).push({});
Nếu hiệu trên âm thì dãy số là dãy số giảm.
Nếu hiệu trên bằng 0 thì dãy số là dãy ko đổi.
*) Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho un ≤ M ∀n ∈ N∗
Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho un ≥ m ∀n ∈ N∗
Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số M, m sao cho m ≤ un ≤ M ∀n ∈ N∗
(adsbygoogle = window.adsbygoogle || []).push({});
⇒ un + 1 > un với mọi n ∈ N
⇒ (un) là dãy tăng.
+ Xét tính bị chặn:
(un) là dãy tăng
⇒ u1 = 2 2 3 n ∀n ∈ N*
⇒ un ≥ 2 ∀n ∈ N*
⇒ (un) bị chặn dưới.
(un) ko bị chặn trên.
⇒ un ko bị chặn.
Suy ra: Với n chẵn ⇒ n – 1 lẻ ⇒ (-1)n – 1 = -1 ⇒ un
Với n lẻ ⇒ n – 1 chẵn ⇒ (-1)n – 1 = 1 ⇒ un > 0.
⇒ u1 > u2 3 > u4 5 > u6 …
⇒ (un) ko tăng ko giảm.
+ Xét tính bị chặn :
Với ∀ n ∈ N:
⇒ -1 ≤ un ≤ 1.
Vậy (un) bị chặn.
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
⇒ un + 1 n với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 – 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Xem toàn thể Giải Toán 11: Ôn tập chương 3
Đăng bởi: Trường THPT Trần Hưng Đạo
Phân mục: Lớp 11, Toán 11
[/toggle]
Bạn thấy bài viết Bài 7 trang 107 SGK Đại số 11 có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về Bài 7 trang 107 SGK Đại số 11 bên dưới để Trường THPT Trần Hưng Đạo có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website của Trường Trường THPT Trần Hưng Đạo
Phân mục: Giáo dục
#Bài #trang #SGK #Đại #số

Trả lời