Bội số chung nhỏ nhất của lớp 6 là một trong những kiến thức toán cơ bản nhưng các em sẽ được làm quen, học và làm các bài tập. Đồng thời, đây cũng là dạng bài tập xuất hiện nhiều trong các kỳ thi.
Bội số chung nhỏ nhất là gì? Cách giải toán lớp 6 bội số chung và bội số chung nhỏ nhất? Hãy cùng Trường THPT Trần Hưng Đạo tìm hiểu cụ thể qua bài viết sau.
Bội số chung nhỏ nhất và bội số chung nhỏ nhất là gì?
Trong chương trình toán lớp 6, các em sẽ được làm quen và học các bài học về bội chung và bội nhỏ nhất. Đặc trưng:
Bội số chung là gì?
Bội số chung được gọi là các số nguyên dương chia hết cho hai hoặc nhiều số nguyên phân biệt. Đặc trưng, cho số tự nhiên 1 chia hết cho số tự nhiên b, hiện thời ta biết a là bội của b.
Bội số chung nhỏ nhất là gì?
Bội số chung nhỏ nhất (BCNN) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho a và b. Tức là BCNN là các số chia hết cho a và b ko dư. Trong trường hợp a hoặc b bằng 0 thì sẽ ko có câu lệnh trạng thái.
Biểu tượng
Bội số chung nhỏ nhất của hai số a và b sẽ được ký hiệu như sau: [a, b]Bảng hợp lý trạng thái (a, b).
Ví dụ: State Report (5, 10, 20) = State Report (5, 10), State Report (10, 2) = 20;
Tìm BCNN của hai số lúc nào?
Trước lúc học cách tìm bội chung nhỏ nhất lớp 6, yêu cầu các em học trò phải biết lúc nào cần tìm BCNN. Cụ thể, BCNN của hai số là Dạng kiến thức được vận dụng trong nhiều bài tập không giống nhau từ dạng số nguyên, dạng lũy thừa, dạng phân số,… để có thể rút gọn số một cách nhanh chóng.
Đặc trưng, ở dạng toán rút gọn phân số, việc tìm BPTNMT giúp ích rất nhiều cho các em có thể giảm phân số về dạng đơn giản nhất để thực hiện phép tính nhanh hơn. Và các bài toán về số nguyên cũng có thể tìm BCNN để dễ tính hơn.

Làm thế nào để tìm bội số chung nhỏ nhất của lớp 6?
Trong môn toán lớp 6, bội chung và bội nhỏ nhất, để tìm NN của hai hay nhiều số lớn hơn 1, người ta chỉ cần vận dụng 3 bước sau:
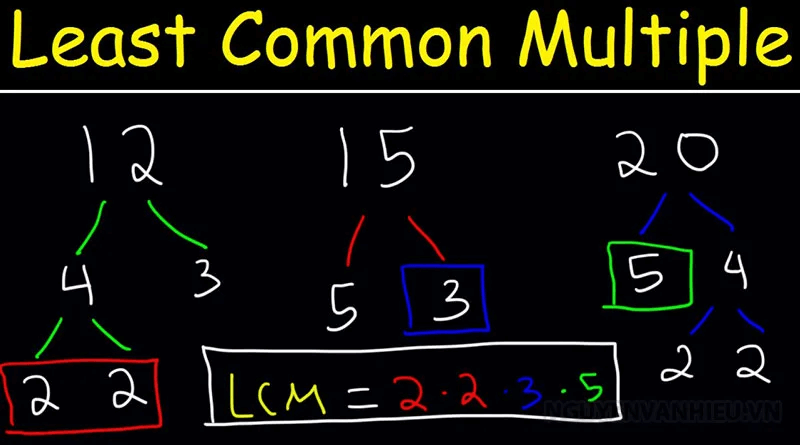
Bước 1: Thực hiện tính từng thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Khởi đầu tích của các thừa số đã chọn, sau đó mỗi thừa số được lấy về số mũ lớn nhất của nó. Lúc này, thành phầm đó chính là BCNN cần tìm.
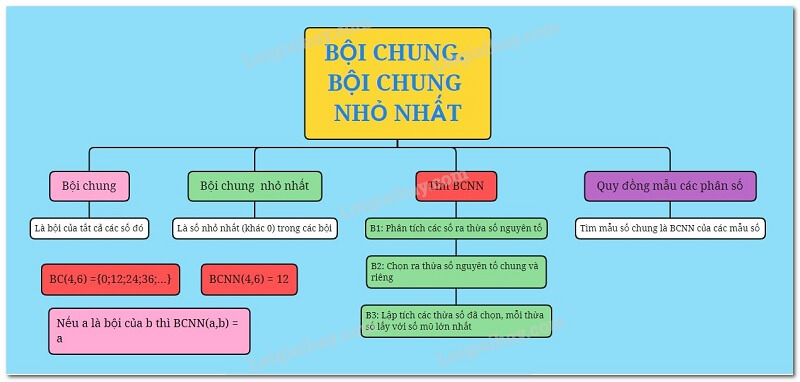
Chú ý:
- Nếu các số đã cho là nguyên tố cùng nhau thì BCNN cần tìm là tích của các số đó.
- Với các số đã cho, nếu số lớn nhất là bội chung của các số còn lại thì phát biểu yêu cầu là số lớn nhất.
Ví dụ:
BCNN (5, 7) = 5,7 = 35. Vì 5 và 7 đều là số nguyên tố nên BCNN là tích của hai số đó, là 35.
Bảng trạng thái (8, 12, 96) = 96. Vì 96 chia hết cho 8 và 12 nên hiện thời muốn tìm phương trình trạng thái của 3 số thì số lớn nhất là 96.
Tìm trị giá của câu lệnh trạng thái (8,9,21).
Trước tiên, người ta cần phân tích các số nguyên đã cho thành lũy thừa của các số nguyên tố. Với mỗi số tìm được, bạn sẽ tính được lũy thừa cao nhất, tích của chúng chính là BCNN nhưng bạn đang tìm. Cụ thể là 2, 3, 5 và 7, mức cao nhất lúc này tuần tự là 23, 32, 30, 71. Lúc này ta thấy bảng hợp lý trạng thái (8, 9, 21) chuẩn xác là 8.9.1.7 = 504.
Các dạng bài tập bội chung và bội nhỏ nhất lớp 6
Đối với môn Toán bội số chung và bội số chung nhỏ nhất lớp 6, sẽ có nhiều dạng bài tập không giống nhau để các em đoạt được, cụ thể:

Dạng 1: Dạng bài toán tìm NN của một số cho trước
Với dạng bài tập này sẽ yêu cầu học trò tìm bội chung nhỏ nhất của 2 hay nhiều số. Cách giải cũng khá đơn giản, học trò chỉ cần vận dụng thứ tự tìm bội chung nhỏ nhất của lớp 6 ở trên là có thể tìm được đáp án chuẩn xác.
Ví dụ: Tìm số dư trạng thái của 30 và 150
Bài giải: BCNN (30, 150) = 150 vì 150 chia hết cho 30;
Dạng 2: Bài toán tìm LCC của một số cho trước
Với dạng bài tập tìm bội nhỏ nhất này, học trò cần phân tích đề, sau đó mở đầu suy luận về việc tìm Dãy của 2 hay nhiều số chuẩn xác.
Ở dạng này, bạn phải phân tích bài toán và suy luận để tìm số dư trạng thái của hai hoặc nhiều số.
Ví dụ: Tìm số tự nhiên nhỏ nhất khác ko a, biết a chia hết cho 15 và 18.
Phần thưởng:
a chia hết cho 15 và 18 nên a được coi là bội chung của 15 và 18.
a là số nhỏ nhất khác 0 nên ta có thể suy ra a là BCNN (15, 18) = 90.
Dạng 3: Tìm NN của hai hay nhiều số thỏa mãn một số điều kiện
Với dạng bài tập này, học trò cũng cần phân tích đề, sau đó sẽ suy luận và đưa về dạng tìm số nhỏ hoặc nhiều số đã cho. Đảm bảo:
Tìm bảng hợp lý của các số đó;
Tìm bội số của BCNN này;
Chọn trong số chúng các bội số thỏa mãn điều kiện đã cho.
Ví dụ: Học trò lớp 6A lúc xếp 2, 3, 4, 8 đều thẳng hàng. Biết rằng số học trò của lớp 6A có khoảng 35-60 học trò. Tổng số học trò của lớp 6A là bao nhiêu?
Phần thưởng:
Dựa vào bài toán ta biết số học trò của lớp 6A phải chia hết cho 2, 3, 4 và 8. Hiện giờ ta phải tìm một số là bội chung của các số đó. Đặc trưng:
Báo cáo trạng thái (2, 3, 4, 8) = 24; Vì vậy, B (24) = {0; 24; 48; 72; 96; …}
Ngoài ra, bài toán còn cho số học trò của lớp 6A trong vòng 35 – 60 nên với các số trong B (24) ở trên chỉ có 48 là thỏa mãn. Lúc này tổng số học trò của lớp 6A tuần tự là 48 học trò.
Bài tập bội chung nhỏ nhất lớp 6 cho các em tự luyện tập
Dưới đây là một số bài tập toán lớp 6 về bội chung và bội ít nhất để các em cùng nhau luyện tập hiệu quả.

Sự kết luận
Đây là thông tin giúp mọi người hiểu rõ hơn về kiến thức Bội số chung và bội số chung nhỏ nhất của lớp 6. Đây là dạng kiến thức quan trọng, thường xuyên xuất hiện trong nhiều đề thi nên các bạn cần luyện tập và vận dụng cách tra cứu nhưng Trường THPT Trần Hưng Đạo san sớt trên đây để có thể đoạt được dạng này một cách hiệu quả.
[toggle title=”xem thêm thông tin chi tiết về Tất tần tật kiến thức về bội chung nhỏ nhất toán lớp 6″ state=”close”]
Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6
Hình Ảnh về: Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6
Video về: Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6
Wiki về Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6
Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6 -
Bội số chung nhỏ nhất của lớp 6 là một trong những kiến thức toán cơ bản nhưng các em sẽ được làm quen, học và làm các bài tập. Đồng thời, đây cũng là dạng bài tập xuất hiện nhiều trong các kỳ thi.
Bội số chung nhỏ nhất là gì? Cách giải toán lớp 6 bội số chung và bội số chung nhỏ nhất? Hãy cùng Trường THPT Trần Hưng Đạo tìm hiểu cụ thể qua bài viết sau.
Bội số chung nhỏ nhất và bội số chung nhỏ nhất là gì?
Trong chương trình toán lớp 6, các em sẽ được làm quen và học các bài học về bội chung và bội nhỏ nhất. Đặc trưng:
Bội số chung là gì?
Bội số chung được gọi là các số nguyên dương chia hết cho hai hoặc nhiều số nguyên phân biệt. Đặc trưng, cho số tự nhiên 1 chia hết cho số tự nhiên b, hiện thời ta biết a là bội của b.
Bội số chung nhỏ nhất là gì?
Bội số chung nhỏ nhất (BCNN) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho a và b. Tức là BCNN là các số chia hết cho a và b ko dư. Trong trường hợp a hoặc b bằng 0 thì sẽ ko có câu lệnh trạng thái.
Biểu tượng
Bội số chung nhỏ nhất của hai số a và b sẽ được ký hiệu như sau: [a, b]Bảng hợp lý trạng thái (a, b).
Ví dụ: State Report (5, 10, 20) = State Report (5, 10), State Report (10, 2) = 20;
Tìm BCNN của hai số lúc nào?
Trước lúc học cách tìm bội chung nhỏ nhất lớp 6, yêu cầu các em học trò phải biết lúc nào cần tìm BCNN. Cụ thể, BCNN của hai số là Dạng kiến thức được vận dụng trong nhiều bài tập không giống nhau từ dạng số nguyên, dạng lũy thừa, dạng phân số,… để có thể rút gọn số một cách nhanh chóng.
Đặc trưng, ở dạng toán rút gọn phân số, việc tìm BPTNMT giúp ích rất nhiều cho các em có thể giảm phân số về dạng đơn giản nhất để thực hiện phép tính nhanh hơn. Và các bài toán về số nguyên cũng có thể tìm BCNN để dễ tính hơn.

Làm thế nào để tìm bội số chung nhỏ nhất của lớp 6?
Trong môn toán lớp 6, bội chung và bội nhỏ nhất, để tìm NN của hai hay nhiều số lớn hơn 1, người ta chỉ cần vận dụng 3 bước sau:
Bước 1: Thực hiện tính từng thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Khởi đầu tích của các thừa số đã chọn, sau đó mỗi thừa số được lấy về số mũ lớn nhất của nó. Lúc này, thành phầm đó chính là BCNN cần tìm.

Chú ý:
- Nếu các số đã cho là nguyên tố cùng nhau thì BCNN cần tìm là tích của các số đó.
- Với các số đã cho, nếu số lớn nhất là bội chung của các số còn lại thì phát biểu yêu cầu là số lớn nhất.
Ví dụ:
BCNN (5, 7) = 5,7 = 35. Vì 5 và 7 đều là số nguyên tố nên BCNN là tích của hai số đó, là 35.
Bảng trạng thái (8, 12, 96) = 96. Vì 96 chia hết cho 8 và 12 nên hiện thời muốn tìm phương trình trạng thái của 3 số thì số lớn nhất là 96.
Tìm trị giá của câu lệnh trạng thái (8,9,21).
Trước tiên, người ta cần phân tích các số nguyên đã cho thành lũy thừa của các số nguyên tố. Với mỗi số tìm được, bạn sẽ tính được lũy thừa cao nhất, tích của chúng chính là BCNN nhưng bạn đang tìm. Cụ thể là 2, 3, 5 và 7, mức cao nhất lúc này tuần tự là 23, 32, 30, 71. Lúc này ta thấy bảng hợp lý trạng thái (8, 9, 21) chuẩn xác là 8.9.1.7 = 504.
Các dạng bài tập bội chung và bội nhỏ nhất lớp 6
Đối với môn Toán bội số chung và bội số chung nhỏ nhất lớp 6, sẽ có nhiều dạng bài tập không giống nhau để các em đoạt được, cụ thể:

Dạng 1: Dạng bài toán tìm NN của một số cho trước
Với dạng bài tập này sẽ yêu cầu học trò tìm bội chung nhỏ nhất của 2 hay nhiều số. Cách giải cũng khá đơn giản, học trò chỉ cần vận dụng thứ tự tìm bội chung nhỏ nhất của lớp 6 ở trên là có thể tìm được đáp án chuẩn xác.
Ví dụ: Tìm số dư trạng thái của 30 và 150
Bài giải: BCNN (30, 150) = 150 vì 150 chia hết cho 30;
Dạng 2: Bài toán tìm LCC của một số cho trước
Với dạng bài tập tìm bội nhỏ nhất này, học trò cần phân tích đề, sau đó mở đầu suy luận về việc tìm Dãy của 2 hay nhiều số chuẩn xác.
Ở dạng này, bạn phải phân tích bài toán và suy luận để tìm số dư trạng thái của hai hoặc nhiều số.
Ví dụ: Tìm số tự nhiên nhỏ nhất khác ko a, biết a chia hết cho 15 và 18.
Phần thưởng:
a chia hết cho 15 và 18 nên a được coi là bội chung của 15 và 18.
a là số nhỏ nhất khác 0 nên ta có thể suy ra a là BCNN (15, 18) = 90.
Dạng 3: Tìm NN của hai hay nhiều số thỏa mãn một số điều kiện
Với dạng bài tập này, học trò cũng cần phân tích đề, sau đó sẽ suy luận và đưa về dạng tìm số nhỏ hoặc nhiều số đã cho. Đảm bảo:
Tìm bảng hợp lý của các số đó;
Tìm bội số của BCNN này;
Chọn trong số chúng các bội số thỏa mãn điều kiện đã cho.
Ví dụ: Học trò lớp 6A lúc xếp 2, 3, 4, 8 đều thẳng hàng. Biết rằng số học trò của lớp 6A có khoảng 35-60 học trò. Tổng số học trò của lớp 6A là bao nhiêu?
Phần thưởng:
Dựa vào bài toán ta biết số học trò của lớp 6A phải chia hết cho 2, 3, 4 và 8. Hiện giờ ta phải tìm một số là bội chung của các số đó. Đặc trưng:
Báo cáo trạng thái (2, 3, 4, 8) = 24; Vì vậy, B (24) = {0; 24; 48; 72; 96; …}
Ngoài ra, bài toán còn cho số học trò của lớp 6A trong vòng 35 - 60 nên với các số trong B (24) ở trên chỉ có 48 là thỏa mãn. Lúc này tổng số học trò của lớp 6A tuần tự là 48 học trò.
Bài tập bội chung nhỏ nhất lớp 6 cho các em tự luyện tập
Dưới đây là một số bài tập toán lớp 6 về bội chung và bội ít nhất để các em cùng nhau luyện tập hiệu quả.

Sự kết luận
Đây là thông tin giúp mọi người hiểu rõ hơn về kiến thức Bội số chung và bội số chung nhỏ nhất của lớp 6. Đây là dạng kiến thức quan trọng, thường xuyên xuất hiện trong nhiều đề thi nên các bạn cần luyện tập và vận dụng cách tra cứu nhưng Trường THPT Trần Hưng Đạo san sớt trên đây để có thể đoạt được dạng này một cách hiệu quả.
[rule_{ruleNumber}]
[box type=”note” align=”” class=”” ltr”>Bội số chung nhỏ nhất và bội số chung nhỏ nhất là gì?
Trong chương trình toán lớp 6, các em sẽ được làm quen và học các bài học về bội chung và bội nhỏ nhất. Đặc biệt:

Bội số chung là gì?
Bội số chung được gọi là tập hợp các số nguyên dương chia hết cho hai hoặc nhiều số nguyên phân biệt. Đặc biệt, cho số tự nhiên 1 chia hết cho số tự nhiên b, bây giờ ta biết a là bội của b.
Bội số chung nhỏ nhất là gì?
Bội số chung nhỏ nhất (BCNN) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho a và b. Tức là BCNN là các số chia hết cho a và b không dư. Trong trường hợp a hoặc b bằng 0 thì sẽ không có câu lệnh trạng thái.
Biểu tượng
Bội số chung nhỏ nhất của hai số a và b sẽ được ký hiệu như sau: [a, b]Bảng hợp lý trạng thái (a, b).
Ví dụ: State Report (5, 10, 20) = State Report (5, 10), State Report (10, 2) = 20;
Tìm BCNN của hai số lúc nào?
Trước lúc học cách tìm bội chung nhỏ nhất lớp 6, yêu cầu các em học trò phải biết lúc nào cần tìm BCNN. Cụ thể, BCNN của hai số là Dạng kiến thức được vận dụng trong nhiều bài tập không giống nhau từ dạng số nguyên, dạng lũy thừa, dạng phân số,… để có thể rút gọn số một cách nhanh chóng.
Đặc trưng, ở dạng toán rút gọn phân số, việc tìm BPTNMT giúp ích rất nhiều cho các em có thể giảm phân số về dạng đơn giản nhất để thực hiện phép tính nhanh hơn. Và các bài toán về số nguyên cũng có thể tìm BCNN để dễ tính hơn.

Làm thế nào để tìm bội số chung nhỏ nhất của lớp 6?
Trong môn toán lớp 6, bội chung và bội nhỏ nhất, để tìm NN của hai hay nhiều số lớn hơn 1, người ta chỉ cần vận dụng 3 bước sau:
Bước 1: Thực hiện tính từng thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Khởi đầu tích của các thừa số đã chọn, sau đó mỗi thừa số được lấy về số mũ lớn nhất của nó. Lúc này, thành phầm đó chính là BCNN cần tìm.

Chú ý:
- Nếu các số đã cho là nguyên tố cùng nhau thì BCNN cần tìm là tích của các số đó.
- Với các số đã cho, nếu số lớn nhất là bội chung của các số còn lại thì phát biểu yêu cầu là số lớn nhất.
Ví dụ:
BCNN (5, 7) = 5,7 = 35. Vì 5 và 7 đều là số nguyên tố nên BCNN là tích của hai số đó, là 35.
Bảng trạng thái (8, 12, 96) = 96. Vì 96 chia hết cho 8 và 12 nên hiện thời muốn tìm phương trình trạng thái của 3 số thì số lớn nhất là 96.
Tìm trị giá của câu lệnh trạng thái (8,9,21).
Trước tiên, người ta cần phân tích các số nguyên đã cho thành lũy thừa của các số nguyên tố. Với mỗi số tìm được, bạn sẽ tính được lũy thừa cao nhất, tích của chúng chính là BCNN nhưng bạn đang tìm. Cụ thể là 2, 3, 5 và 7, mức cao nhất lúc này tuần tự là 23, 32, 30, 71. Lúc này ta thấy bảng hợp lý trạng thái (8, 9, 21) chuẩn xác là 8.9.1.7 = 504.
Các dạng bài tập bội chung và bội nhỏ nhất lớp 6
Đối với môn Toán bội số chung và bội số chung nhỏ nhất lớp 6, sẽ có nhiều dạng bài tập không giống nhau để các em đoạt được, cụ thể:

Dạng 1: Dạng bài toán tìm NN của một số cho trước
Với dạng bài tập này sẽ yêu cầu học trò tìm bội chung nhỏ nhất của 2 hay nhiều số. Cách giải cũng khá đơn giản, học trò chỉ cần vận dụng thứ tự tìm bội chung nhỏ nhất của lớp 6 ở trên là có thể tìm được đáp án chuẩn xác.
Ví dụ: Tìm số dư trạng thái của 30 và 150
Bài giải: BCNN (30, 150) = 150 vì 150 chia hết cho 30;
Dạng 2: Bài toán tìm LCC của một số cho trước
Với dạng bài tập tìm bội nhỏ nhất này, học trò cần phân tích đề, sau đó mở đầu suy luận về việc tìm Dãy của 2 hay nhiều số chuẩn xác.
Ở dạng này, bạn phải phân tích bài toán và suy luận để tìm số dư trạng thái của hai hoặc nhiều số.
Ví dụ: Tìm số tự nhiên nhỏ nhất khác ko a, biết a chia hết cho 15 và 18.
Phần thưởng:
a chia hết cho 15 và 18 nên a được coi là bội chung của 15 và 18.
a là số nhỏ nhất khác 0 nên ta có thể suy ra a là BCNN (15, 18) = 90.
Dạng 3: Tìm NN của hai hay nhiều số thỏa mãn một số điều kiện
Với dạng bài tập này, học trò cũng cần phân tích đề, sau đó sẽ suy luận và đưa về dạng tìm số nhỏ hoặc nhiều số đã cho. Đảm bảo:
Tìm bảng hợp lý của các số đó;
Tìm bội số của BCNN này;
Chọn trong số chúng các bội số thỏa mãn điều kiện đã cho.
Ví dụ: Học trò lớp 6A lúc xếp 2, 3, 4, 8 đều thẳng hàng. Biết rằng số học trò của lớp 6A có khoảng 35-60 học trò. Tổng số học trò của lớp 6A là bao nhiêu?
Phần thưởng:
Dựa vào bài toán ta biết số học trò của lớp 6A phải chia hết cho 2, 3, 4 và 8. Hiện giờ ta phải tìm một số là bội chung của các số đó. Đặc trưng:
Báo cáo trạng thái (2, 3, 4, 8) = 24; Vì vậy, B (24) = {0; 24; 48; 72; 96; …}
Ngoài ra, bài toán còn cho số học trò của lớp 6A trong vòng 35 – 60 nên với các số trong B (24) ở trên chỉ có 48 là thỏa mãn. Lúc này tổng số học trò của lớp 6A tuần tự là 48 học trò.
Bài tập bội chung nhỏ nhất lớp 6 cho các em tự luyện tập
Dưới đây là một số bài tập toán lớp 6 về bội chung và bội ít nhất để các em cùng nhau luyện tập hiệu quả.

Sự kết luận
Đây là thông tin giúp mọi người hiểu rõ hơn về kiến thức Bội số chung và bội số chung nhỏ nhất của lớp 6. Đây là dạng kiến thức quan trọng, thường xuyên xuất hiện trong nhiều đề thi nên các bạn cần luyện tập và vận dụng cách tra cứu nhưng Trường THPT Trần Hưng Đạo san sớt trên đây để có thể đoạt được dạng này một cách hiệu quả.
[/box]
#Tất #tần #tật #kiến #thức #về #bội #chung #nhỏ #nhất #toán #lớp
[/toggle]
Bạn thấy bài viết Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6 có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về Tất tần tật tri thức về bội chung nhỏ nhất toán lớp 6 bên dưới để thpttranhungdao.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho độc giả nhé! Cám ơn bạn đã ghé thăm Website Trường THPT Trần Hưng Đạo
Phân mục: Giáo dục
#Tất #tần #tật #kiến #thức #về #bội #chung #nhỏ #nhất #toán #lớp


Trả lời